Coherent Noise
To generate a noisy image, each pixel is allocated a level of greyness between 0 (black) and 255 (white).
A Pseudo Random Number Generator (PRNG) is usually intended to be as random as possible and generates an image like this:
 If the Seed concept is removed, a PRNG that could provide a number for a given coordinate would allow the creation of the same noisy image in each area of space.
That is the first step that gives us control of the image created. The following PRNG algorithm returns a parameter in the interval [0,1] which makes mixing values easy (there will be a lot of mixing).
If the Seed concept is removed, a PRNG that could provide a number for a given coordinate would allow the creation of the same noisy image in each area of space.
That is the first step that gives us control of the image created. The following PRNG algorithm returns a parameter in the interval [0,1] which makes mixing values easy (there will be a lot of mixing).
double Noise::NoiseFunction(DWORD x) {
x=(x<<13)^x;
return ((x*(x*x*15731+789221)+1376312589)&LONG_MAX)/double(LONG_MAX);
}
Useful noise needs to look more like the surface of an ocean, having visible large waves with many smaller waves on them...
The big waves don't need many random numbers, so instead of asking for a number every pixel, use the same number for a block of pixels.
First a look at what we get with the above PRNG alone:
for(WORD x=GetWidth(); x--;) {
double u=Noise::NoiseFunction(x);
for(WORD y=GetHeight(); y--;) {
double v=Noise::NoiseFunction(y);
BYTE B=BYTE(Round(255*u));
SetPixel(x,y, RGB(B,B,B));
}
SetPixel(x, GetHeight()*(1-u), 0xFF0000);
}
GetWidth(), GetHeight() and SetPixel are members of CPixelBlock which was used as a base class.
Round is declared in Global.h.
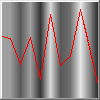
Predictably, the columns are normal ugly random noise values and look like a bar-code:
 The red dots are a graph of whiteness: a dot at the bottom is a black column, a dot at the top is a white column (they look better later when the noise is less noisy).
The red dots are a graph of whiteness: a dot at the bottom is a black column, a dot at the top is a white column (they look better later when the noise is less noisy).
The image can be scaled if the integer passed to the call to the NoiseFunction changes for a block of pixels:
for(WORD x=GetWidth(); x--;) {
double u=Noise::NoiseFunction(x/10);
for(WORD y=GetHeight(); y--;) {
BYTE B=BYTE(Round(255*u));
SetPixel(x,y, RGB(B,B,B));
}
SetPixel(x, GetHeight()*(1-u), 0xFF0000);
}
Now the zoomed-in image is something that could potentially be smoothed into waves:
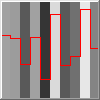
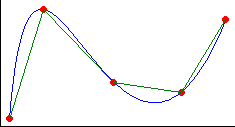
The last stages are to join the dots by Interpolating between them (the green lines) and then smoothing (the blue curve):
for(WORD x=GetWidth(); x--;) {
int X=Floor(x/10.0);
double u=Noise::NoiseFunction(X);
double u1=Noise::NoiseFunction(1+X);
u=Interpolate(x/10.0-X, u,u1);
for(WORD y=GetHeight(); y--;) {
BYTE B=BYTE(Round(255*u));
SetPixel(x,y, RGB(B,B,B));
}
SetPixel(x, GetHeight()*(1-u), 0xFF0000);
}
Interpolate and Floor are declared in Global.h.
This now looks like smooth random waves, but you can see from the red dots (which have been joined with lines) that the waves are sharply pointed.
Improving the Smoothing
The following code shows a quick method to smooth the noise by mixing in adjacent noise values.
Two adjacent SmoothedNoise values are interpolated using the fractional part of the double, x.
double Noise::SmoothedNoise(DWORD x) {return NoiseFunction(x)/2 + NoiseFunction(x-1)/4 + NoiseFunction(x+1)/4;}
double Noise::InterpolatedNoise(double x) {
DWORD X=Floor(x);
return Interpolate(x-X, SmoothedNoise(X), SmoothedNoise(X+1));
}
It is important to understand the scale here: it is still smoothing zoomed-in bars as in the original example:

The integer part of the double, x, that is passed to InterpolatedNoise, should be constant across one bar, and the fractional part is a parameter in the range [0,1] crossing each bar.
The x parameter has been scaled 30 times here:
for(WORD x=GetWidth(); x--;) {
double u=double(x)/GetWidth();
u=Noise::InterpolatedNoise(u*30);
for(WORD y=GetHeight(); y--;) {
BYTE B=BYTE(Round(255*u));
SetPixel(x,y, RGB(B,B,B));
}
SetPixel(x, GetHeight()*(1-u), 0xFF0000);
}
Now the image is properly random smooth waves, but notice that the range is not likely to go to full black or white:
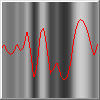
Ripples on Waves
If the 30 scale factor were changed to 60 another image would be generated with smaller blocks which would make smaller waves.
If a number of iterations are done with finer and finer block sizes, and iterations are all mixed together, the result is like the initial ocean analogy: little waves are added on the back of the big waves and you have coherent noise.
Mixing the different wave sizes is done using a simple loop that will collect a noise sample at a particular coordinate for a particular wave size.
The wave sizes get halved each iteration (Frequency gets doubled) so the iterations are known as Octaves (from music, a note an octave higher has double the frequency).
The following code will collect three octaves per pixel, starting with the biggest waves and mixing in smaller waves at each iteration.
Level of Detail refers to the amount that gets mixed in at each level: the values here mean that four octaves will be collected,
the first octave at full amplitude, the second octave will have half its amplitude mixed in (Persistence=0.5), the third octave a quarter (Persistence*Persistence) and the fourth, an eighth (Persistence*Persistence*Persistence):
for(WORD x=W->GetWidth(); x--;) {
int Octaves=4;
double Persistence=0.5;
double u=double(x)/W->GetWidth();
double Result=0;
DWORD Frequency=1;
for(double Amplitude=1; (Octaves--) && (Amplitude>1/256.); Amplitude*=Persistence, Frequency<<=1) {
Result+=Amplitude * Noise::InterpolatedNoise((u*30)*Frequency);
}
Result=Unsigned(Result);
for(WORD y=W->GetHeight(); y--;) {
BYTE B=BYTE(Round(255*Result));
W->SetPixel(x,y, RGB(B,B,B));
} }
This generates one-dimensional coherent noise which can be seen here as each octave gets mixed in:


Uses
This ability to generate random waves with programable waviness can be used anywhere that you want to introduce a natural look or feel:
for example camera movement in a game can be made less stable with controlled random movements.
Regular patterns can be given more natural spacings, for example, the bricks in this wall are not all perfectly ligned up:

Clearly the wall would benefit from being colored with a mix of shades in random places;
This algorithm can be extended to work in more than one dimension, which leads to the creation of Procedural Textures.
Procedural Textures can create photo-realistic scenery (clouds, land, water), walls and floors (marble, wood-grain, dirt) using these methods.



If something like coherent noise is mixed with the wall image to make it look dirty and a Color Spline:

is used to color it, the potential becomes more obvious:

The Brick Wall Tutorial shows how this image was created.
Another example is the reflection in the Buttons generated by the code on the ButtonStencil page:

The Button Tutorial shows how such buttons are drawn.
Turbulence
The cloud-like textures can be given a turbulent look by folding them using the fabs function:
for(WORD x=W->GetWidth(); x--;) {
int Octaves=4;
double Persistence=0.5;
double u=double(x)/W->GetWidth();
double Result=0;
DWORD Frequency=1;
for(double Amplitude=1; (Octaves--) && (Amplitude>1/256.); Amplitude*=Persistence, Frequency<<=1) {
Result+=Amplitude * fabs(Noise::InterpolatedNoise((u*30)*Frequency));
}
Result=Unsigned(Result);
for(WORD y=W->GetHeight(); y--;) {
BYTE B=BYTE(Round(255*Result));
W->SetPixel(x,y, RGB(B,B,B));
} }

The following animation uses three dimensional noise (time being the third dimension):

The gold menu at the top of this page leads to descriptions of various types of procedural noise.



















 If the
If the  The red dots are a graph of whiteness: a dot at the bottom is a black column, a dot at the top is a white column (they look better later when the noise is less noisy).
The red dots are a graph of whiteness: a dot at the bottom is a black column, a dot at the top is a white column (they look better later when the noise is less noisy).














